Как обозначается угол поворота

Вращательное движение (Движение тела по окружности)

Законы, определяющие движение тела по окружности, аналогичны законам поступательного движения. Уравнения, описывающие вращательное движение, можно вывести из уравнений поступательного движения, произведя в последних следующие замены:

Если:
перемещение s — угловое перемещение (угол поворота) φ,
скорость u — угловая скорость ω,
ускорение a — угловое ускорение α

О матрице поворота простыми словами

Когда Пифагор плыл по реке Хуанхэ, он увидел у берега, в лодке, задремавшего рыбака, в конической шляпе и с бамбуковой удочкой в руках.

Памятуя о том, что на Хабрахабр заглядывают люди разной математической подготовки, — однако, в поле интересов которых вполне может попадать тема линейных преобразований, — в связи с её практической значимостью, — я попробую рассказать об этом максимально доступно.

Синус, косинус, тангенс и котангенс: определения в тригонометрии, примеры, формулы

Тригонометрия – раздел математической науки, в котором изучаются тригонометрические функции и их использование в геометрии. Развитие тригонометрии началось еще во времена античной Греции. Во времена средневековья важный вклад в развитие этой науки внесли ученые Ближнего Востока и Индии.

Данная статья посвящена базовым понятиям и дефинициям тригонометрии. В ней рассмотрены определения основных тригонометрических функций: синуса, косинуса, тангенса и котангенса. Разъяснен и проиллюстрирован их смысл в контексте геометрии.

Необходимо запомнить

Угол поворота – угол, на который поворачивается радиус-вектор, соединяющий центр окружности с точкой тела, движущейся по окружности. $varphi = frac, [varphi] = рад$.

Угловая скорость – отношение угла поворота φ к промежутку времени, в течение которого совершен этот поворот при равномерном движении точки по окружности.

Линейная скорость – отношение длины дуги окружности, пройденной точкой к промежутку времени.

$upsilon = omega R$, $upsilon = frac$, $[upsilon] = м/с$.

Центростремительное ускорение точки, равномерно движущейся по окружности, направлено по радиусу окружности к ее центру и модуль равен

Период – промежуток времени, за который тело делает один полный оборот:

Частота обращения тела – число оборотов за единицу времени.

$
u = frac$, $omega = 2 pi
u$

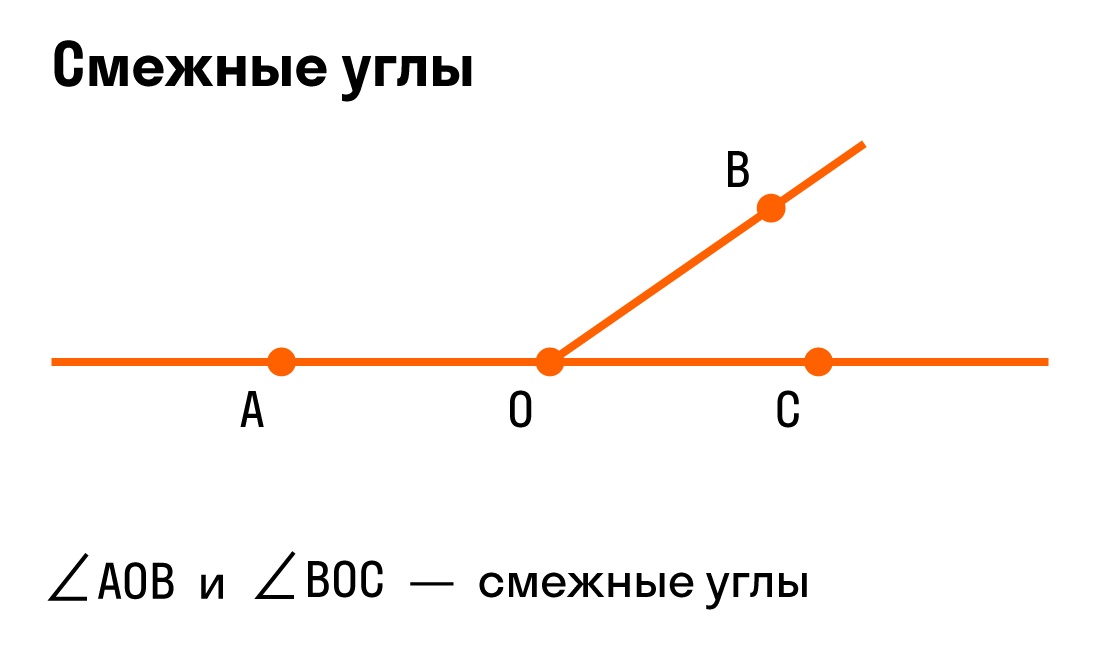
Определение смежных и вертикальных углов

Смежные углы — это пара углов, у которых одна сторона общая, а две другие стороны лежат на одной прямой. Таким образом два смежных угла составляют развернутый угол. Общая сторона двух смежных углов называется наклонной к прямой, на которой лежат другие стороны, при условии, что смежные углы не равны.

Вертикальные углы — это пара углов, у которых есть общая вершина, при этом стороны одного угла составляют продолжение сторон другого угла.

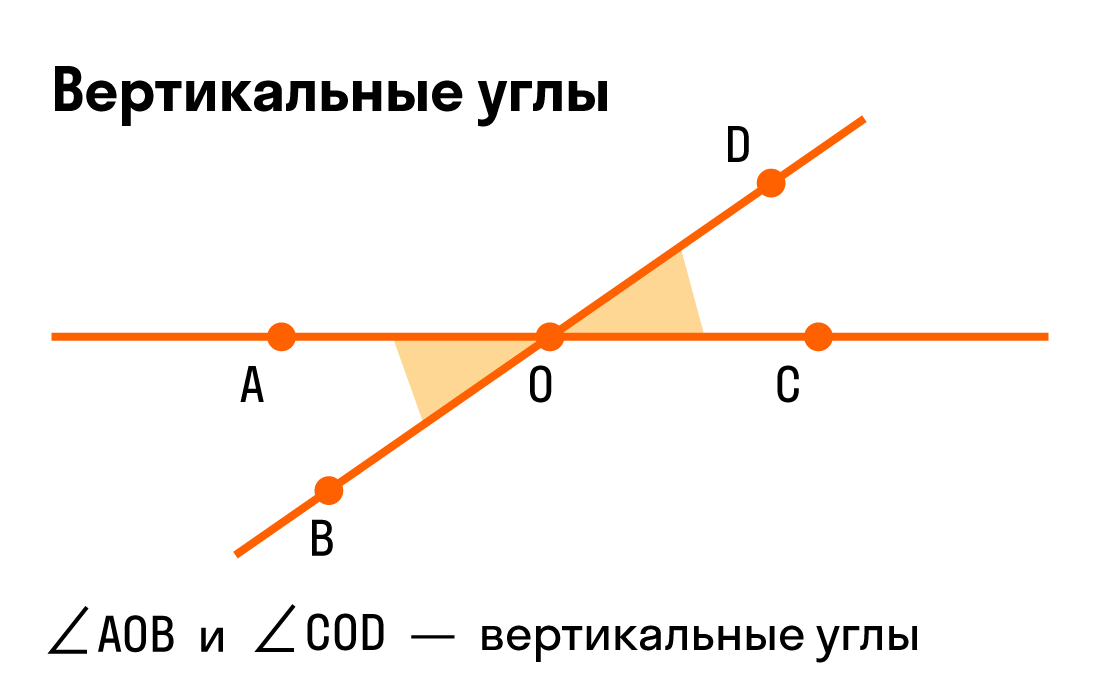
При пересечении прямых получается четыре пары смежных и две пары вертикальных углов. Вот как это выглядит:

1. Схождение

Схождением называют разницу расстояний, измеренных по передним и задним точкам диска колеса в горизонтальной плоскости. Если расстояние, измеренное по передним точкам меньше расстояния, измеренного по задним точкам (т.е. колеса повернуты к центральной линии автомобиля), то говорят о положительном схождении, если наоборот – об отрицательном (обратном) схождении.

До проведения измерений нужно убедиться в отсутствии биения дисков колес. Неправильная регулировка схождения отрицательно влияет на стабилизацию рулевого управления и комфортность управления автомобилем.

Схождение колес может быть выражено в линейных и угловых мерах, в зависимости от типа применяемого оборудования.

Вращательное движение, характеристики

Вращательное движение	Угловая скорость	Угловое ускорение
Равномерное	Постоянная	Равно нулю
Равномерно ускоренное	Изменяется равномерно	Постоянно
Неравномерно ускоренное	Изменяется неравномерно	Переменное

Что называют поворотом точки вокруг точки?

Сразу отметим, что наряду с фразой «поворот вокруг точки» будем также использовать словосочетания «поворот около точки» и «поворот относительно точки», что обозначает одно и то же.

Введем понятие поворота точки вокруг точки.

Сначала дадим определение центра поворота.

Точку, относительно которой осуществляется поворот, называют центром поворота.

Теперь скажем, что получается в результате поворота точки.

В результате поворота некоторой точки A относительно центра поворота O получается точка A₁ (которая в случае некоторого количества полных оборотов может совпадать с A ), причем точка A₁ лежит на окружности с центром в точке O радиуса OA . Иными словами, при повороте относительно точки O точка A переходит в точку A₁ , лежащую на окружности с центром в точке O радиуса OA .

Считают, что точка O при повороте вокруг самой себя переходит в саму себя. То есть, в результате поворота вокруг центра поворота O точка O переходит в саму себя.

Также стоит отметить, что поворот точки А вокруг точки O стоит рассматривать как перемещение в результате движения точки А по окружности с центром в точке O радиуса OA .

Для наглядности приведем иллюстрации поворота точки А вокруг точки O , на рисунках, расположенных ниже, перемещение точки А в точку А₁ покажем при помощи стрелки.

Продолжим историю

Треугольные очертания лодки, шляпы и удочки над водой настолько поразили философа-математика, что он застыл как заворожённый.

Удочка рыбака аккуратно зависла над гладью вод Жёлтой Реки под углом, равным 45 градусам.

Лёгкий туман стелился над водой… и вдруг — поклёв. Рыбак потянул удочку, и она стала быстро набирать высоту, длина лески (катет А) стала расти на глазах, а расстояние от рыбака до самой лески стало уменьшаться (катет B). И самое интересное — длина самой удочки совсем не изменилась — телескопических удочек ещё не было, — даже когда она описала в воздухе дугу и оказалась почти над головой рыбака, под углом 90 градусов. Длина лески сравнялась с длиной удочки — катушки тогда уже были, — а расстояние между рыбаком и леской изменилось до 0, леска оказалась в руках рыбака.

Последний момент очень важен для понимания того, что происходит при умножении вектора-удочки на матрицу поворота.

Ностальгируем и думаем дальше.

Вспомним теорему Пифагора: квадрат длины удочки равен сумме квадратов катетов — самой лески и расстоянию между рыбаком и тем местом, где леска погружена в воду — С^2=А в квадрате + B в квадрате.

Представим, что длина удочки 4.2, длина (или высота над водой) лески 3, расстояние между рыбаком и местом, где леска погружена в воду тоже 3.

Синус, косинус, тангенс и котангенс. Определения

Изначально определения тригонометрических функций, аргументом которых является угол, выражались через соотношения сторон прямоугольного треугольника.

Определения тригонометрических функций

Синус угла ( sin α ) – отношение противолежащего этому углу катета к гипотенузе.

Косинус угла ( cos α ) – отношение прилежащего катета к гипотенузе.

Тангенс угла ( t g α ) – отношение противолежащего катета к прилежащему.

Котангенс угла ( c t g α ) – отношение прилежащего катета к противолежащему.

Данные определения даны для острого угла прямоугольного треугольника!

В треугольнике ABC с прямым углом С синус угла А равен отношению катета BC к гипотенузе AB.

Определения синуса, косинуса, тангенса и котангенса позволяют вычислять значения этих функций по известным длинам сторон треугольника.

Область значений синуса и косинуса: от -1 до 1. Иными словами синус и косинус принимают значения от -1 до 1. Область значений тангенса и котангенса – вся числовая прямая, то есть эти функции могут принимать любые значения.

Решение задачи

Использование сочетания поступательного движения с вращательным

Сочетание поступательного движения с вращательным использовали в технике с давних времён. При установлении в Петербурге памятника Петру I – Медного всадника – строителям нужно было перевезти кусок скалы для постамента массой более тысячи тонн. Колоссальный камень передвигали всего несколько десятков рабочих. При этом были использованы лебёдки и пушечные ядра, уложенные в специальные деревянные жёлоба, окованные с внутренней стороны листовой медью. Лишь использование вращательного движения ядер позволило решить такую трудную по тем временам техническую задачу. Ядра, по существу, выполняли роль шарикоподшипников, широко применяемых в современной технике.

• 1
• 2

2. Обратное схождение в повороте

Обратное схождение в повороте – это разность углов поворота внешнего и внутреннего колеса, отсчитываемых от центральной оси автомобиля.

Рулевое управление сконструировано так, что внутреннее колесо катится по меньшему радиусу поворота (имеет больший угол поворота), что уменьшает проскальзывание колеса.

Разница углов поворота влево и вправо должна быть нулевой или в пределах, допускаемых заводом-изготовителем (угол А)

Полный оборот

Можно выполнить такой поворот точки A относительно центра поворота O , что точка А , пройдя все точки окружности, окажется на прежнем месте. При этом говорят, что точка А совершила полный оборот вокруг точки O .

Дадим графическую иллюстрацию полного оборота.

Если же не останавливаться на одном обороте, а продолжать движение точки по окружности, то можно выполнить два, три и так далее полных оборотов. На чертеже ниже справа показано, как могут быть произведены два полных оборота, а слева — три оборота.

Можно также говорить о частях полного оборота, например, о половине оборота, трети, четверти и т.д. оборота (при надобности смотрите статью доли и обыкновенные дроби).

Угловая скорость

Когда тело движется по окружности, то не все его точки движутся с одинаковой скоростью относительно оси вращения. Если взять лопасти обычного бытового вентилятора, которые вращаются вокруг вала, то точка расположенная ближе к валу имеет скорость вращения больше, чем отмеченная точка на краю лопасти. Это значит, у них разная линейная скорость вращения. В то же время угловая скорость у всех точек одинаковая.

Угловая скорость представляет собой изменение угла в единицу времени, а не расстояния. Обозначается буквой греческого алфавита – ω и имеет единицу измерения радиан в секунду (рад/с). Иными словами, угловая скорость – это вектор, привязанный к оси обращения предмета.

Формула для вычисления отношения между углом поворота и временным интервалом выглядит так:

где:

• ω – угловая скорость (рад./с);
• ∆ϕ – изменение угла отклонения при повороте (рад.);
• ∆t – время, затраченное на отклонение ©.

Обозначение угловой скорости употребляется при изучении законов вращения. Оно употребляется при описании движения всех вращающихся тел.

Угловая скорость в конкретных случаях

На практике редко работают с величинами угловой скорости. Она нужна при конструкторских разработках вращающихся механизмов: редукторов, коробок передач и прочего.

Вычислить её, применяя формулу, можно. Для этого используют связь угловой скорости и частоты вращения.

где:

• π – число, равное 3,14;
• ν – частота вращения, (об./мин.).

В качестве примера могут быть рассмотрены угловая скорость и частота вращения колёсного диска при движении мотоблока. Часто необходимо уменьшить или увеличить скорость механизма. Для этого применяют устройство в виде редуктора, при помощи которого понижают скорость вращения колёс. При максимальной скорости движения 10 км/ч колесо делает около 60 об./мин. После перевода минут в секунды это значение равно 1 об./с. После подстановки данных в формулу получится результат:

ω = 2*π*ν = 2*3,14*1 = 6,28 рад./с.

К сведению. Снижение угловой скорости часто требуется для того, чтобы увеличить крутящий момент или тяговое усилие механизмов.

Как определить угловую скорость

Принцип определения угловой скорости зависит от того, как происходит движение по окружности. Если равномерно, то употребляется формула:

Если нет, то придётся высчитывать значения мгновенной или средней угловой скорости.

Величина, о которой идёт разговор, векторная, и при определении её направления используют правило Максвелла. В просторечии – правило буравчика. Вектор скорости имеет одинаковое направление с поступательным перемещением винта, имеющего правую резьбу.

Рассмотрим на примере, как определить угловую скорость, зная, что угол поворота диска радиусом 0,5 м меняется по закону ϕ = 6*t:

ω = ϕ / t = 6 * t / t = 6 с-1

Вектор ω меняется из-за поворота в пространстве оси вращения и при изменении значения модуля угловой скорости.

НАШИ ПАРТНЁРЫ

© Государственная образовательная платформа «Российская электронная школа»

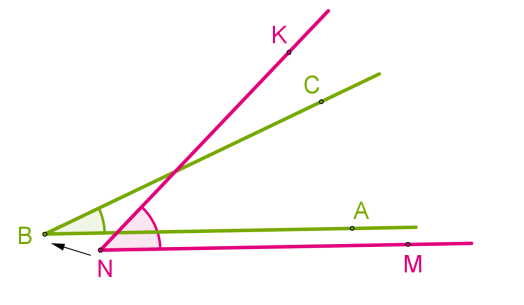
Сравнение углов

Для сравнения углов можно использовать самый простой способ из программы 4 класса — метод наложения. Для этого нужно совместить две вершины и сторону одного угла со стороной другого. Если стороны заданных углов совпадут, значит углы равные. Если нет, то угол, который лежит внутри другого, будет меньшим. Здесь два наглядных примера с равными и неравными углами:

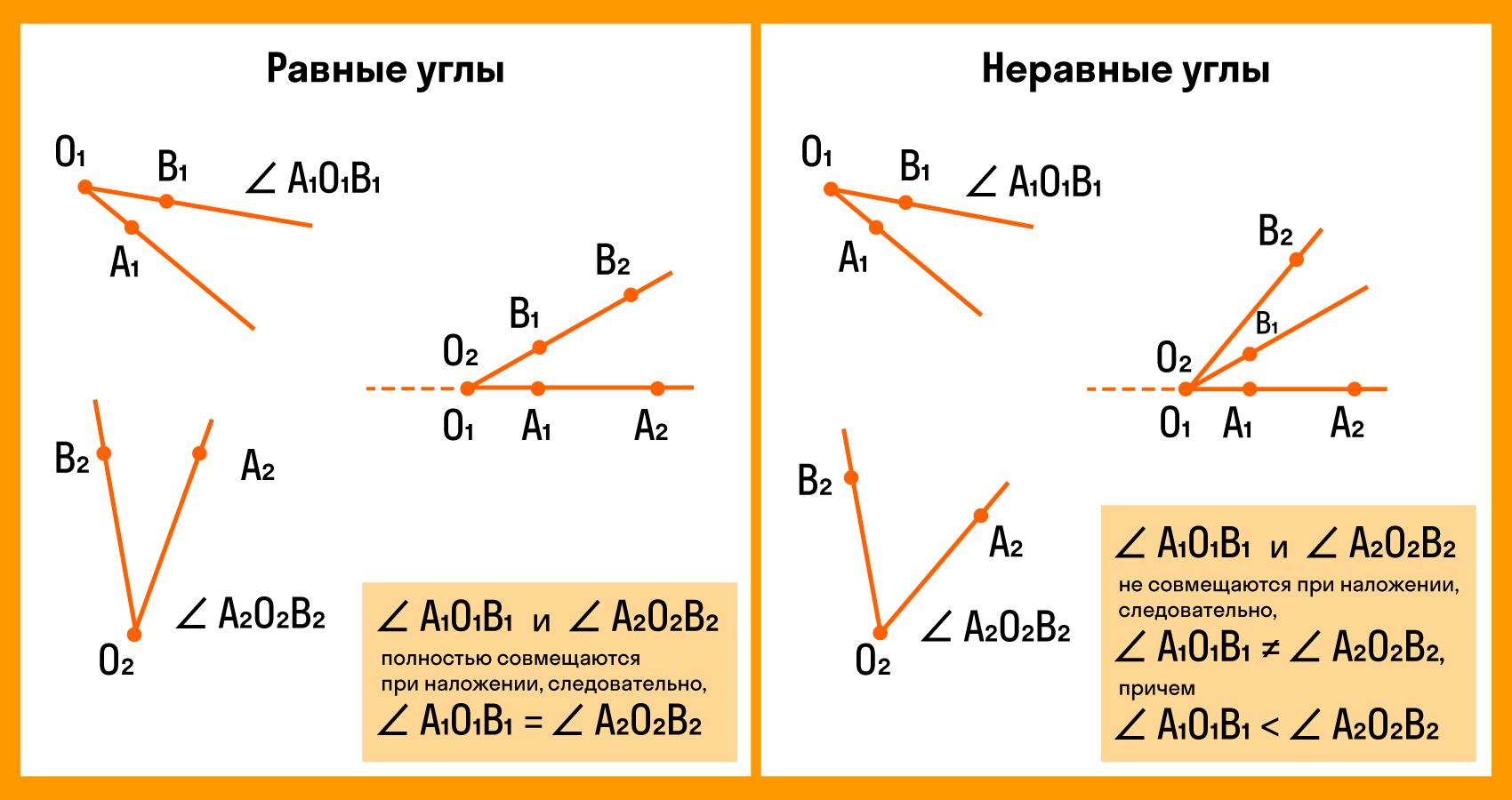
При этом развернутые углы всегда являются равными.

Совмещение углов ∠???????????? и ∠???????????? происходит следующим образом:

1. Вершину ???? одного угла совмещаем с вершиной ???? другого угла.
2. Сторону ???????? одного угла накладываем на сторону ???????? другого угла так, чтобы стороны ???????? и ???????? располагались в одном направлении.

Если совпадут и другие стороны, то углы равны: ∠???????????? = ∠????????????.

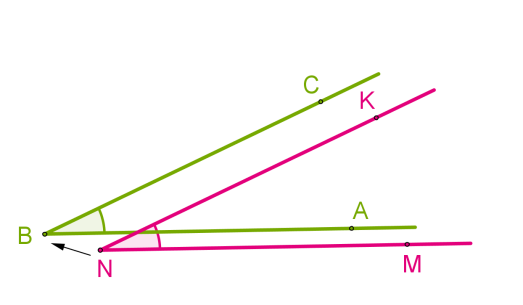
Если нет, то один угол — меньше другого: ∠????????????<∠????????????.

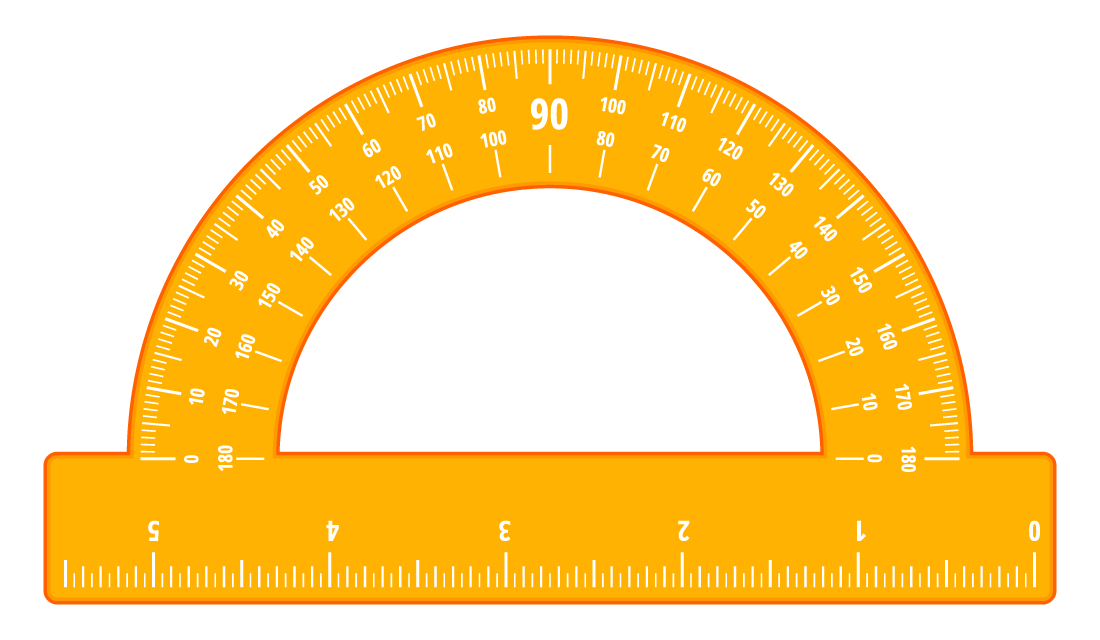
Сравнить углы можно также, измерив их величины. Для этого понадобится специальный инструмент для построения и измерения углов — транспортир. Вот, как он выглядит:

Угол поворота и период обращения

Рассмотрим точку А на предмете, вращающимся вокруг своей оси. При обращении за какой-то период времени она изменит своё положение на линии окружности на определённый угол. Это угол поворота. Он измеряется в радианах, потому что за единицу берётся отрезок окружности, равный радиусу. Ещё одна величина измерения угла поворота – градус.

Когда в результате поворота точка А вернётся на своё прежнее место, значит, она совершила полный оборот. Если её движение повторится n-раз, то говорят о некотором количестве оборотов. Исходя из этого, можно рассматривать ½, ¼ оборота и так далее. Яркий практический пример этому – путь, который проделывает фреза при фрезеровании детали, закреплённой в центре шпинделя станка.

Внимание! Угол поворота имеет направление. Оно отрицательное, когда вращение происходит по часовой стрелке и положительное при вращении против движения стрелки.

Если тело равномерно продвигается по окружности, можно говорить о постоянной угловой скорости при перемещении, ω = const.

В этом случае находят применения такие характеристики, как:

• период обращения – T, это время, необходимое для полного оборота точки при круговом движении;
• частота обращения – ν, это полное количество оборотов, которое совершает точка по круговой траектории за единичный временной интервал.

Интересно. По известным данным, Юпитер обращается вокруг Солнца за 12 лет. Когда Земля за это время делает вокруг Солнца почти 12 оборотов. Точное значение периода обращения круглого гиганта – 11,86 земных лет.

3. Угол развала

Если колесо отклонено от вертикальной плоскости наружу автомобиля, то говорят о положительном развале (В), если колеса отклоняются внутрь – то развал отрицательный (С). При этом направление взгляда – вдоль оси автомобиля спереди назад.

Влияние развала может быть рассмотрено на примере качения конуса А (стабилизация качения). Так, колеса, имеющие положительный развал, имеют тенденцию к качению по направлению от центральной оси автомобиля; колеса, имеющие отрицательный развал, катятся по направлению к центральной оси.

Развал измеряется в градусах, при этом колеса должны находиться в положении прямолинейного движения.

Число оборотов

Характеристикой всех видов вращения является число оборотов n или равноценная ей характеристика — частота f. Обе величины характеризуют число оборотов в единицу времени.

Единица СИ частоты (или числа оборотов)

В технике число оборотов обычно измеряется в оборотах в минуту (об/мин) = 1/мин.

Таким образом, величина, обратная числу оборотов, есть продолжительность одного оборота.

Если
n — число оборотов,
f — частота,
T — продолжительность одного оборота, период,
φ — угловое перемещение,
N — полное число оборотов,
t — время, продолжительность вращения,
ω — угловая частота,
то

Период

Угловое перемещение

Угловое перемещение равно произведению полного числа оборотов на 2π:

Угловая скорость

Из формулы для одного оборота следует:

Обратите внимание:
• формулы (1)—(6) справедливы для всех видов вращательного движения — как для равномерного движения, так и для ускоренного. В них могут входить постоянные величины, средние значения, начальные и конечные значения, а также любые мгновенные значения.
• вопреки своему названию число оборотов n — это не число, а физическая величина.
• следует различать число оборотов n и полное число оборотов N.

Далее

Теперь ещё раз осуществим умножение катета А на sin(a), катета B на cos(a).

Снова получили число равное длине удочки… и мы вплотную подобрались к матрице поворота.

Напомню формулу

(изображение из Википедии. Ссылка на статью)

Возьмём её нижнюю часть — получение точки y:

И сравним с вычислениями выше:

Как две капли воды. Y в нашем случае окажется равным 4.2.
Если применить первую часть формулы к вычислениям, то получим:

Иными словами случится так:

x станет 0 — рыбак поймает леску.
y станет 4.2 — леска сравняется с длиной удочки.

Помним, что для вычисления x синус и косинус меняются местами.

Ф в данном случае равно 45 градусам (Ф = 0.7 ) и при таком угле синус и косинус равны, что удобно для примера. В остальных случаях очевидно величины для синуса и косинуса будут другие. Например, для 40 градусов: cosdegree(40) = 0,7660444431, sindegree(40) = 0,6427876097 (если вы не согласны, обращайтесь в Яндекс, я пользовался его калькулятором).

Числа

Как быть с определением синуса, косинуса, тангенса и котангенса числа, а не угла поворота?

Синус, косинус, тангенс, котангенс числа

Синусом, косинусом, тангенсом и котангенсом числа t называется число, которое соответственно равно синусу, косинусу, тангенсу и котангенсу в t радиан.

Например, синус числа 10 π равен синусу угла поворота величиной 10 π рад.

Существует и другой подход к определению синуса, косинуса, тангенса и котангенса числа. Рассмотрим его подробнее.

Любому действительному числу t ставится в соответствие точка на единичной окружности с центром в начале прямоугольной декартовой системы координат. Синус, косинус, тангенс и котангенс определяются через координаты этой точки.

Начальная точка на окружности – точка A c координатами ( 1 , 0 ).

Положительному числу t соответствует точка, в которую перейдет начальная точка, если будет двигаться по окружности против часовой стрелки и пройдет путь t .

Отрицательному числу t соответствует точка, в которую перейдет начальная точка, если будет двигаться по окружности против часовой стрелки и пройдет путь t .

Теперь, когда связь числа и точки на окружности установлена, переходим к определению синуса, косинуса, тангенса и котангенса.

Синус (sin) числа t

Синус числа t – ордината точки единичной окружности, соответствующей числу t. sin t = y

Косинус числа t – абсцисса точки единичной окружности, соответствующей числу t. cos t = x

Тангенс числа t – отношение ординаты к абсциссе точки единичной окружности, соответствующей числу t. t g t = y x = sin t cos t

Последние определения находятся в соответствии и не противоречат определению, данному в начале это пункта. Точка на окружности, соответствующая числу t, совпадает с точкой, в которую переходит начальная точка после поворота на угол t радиан.

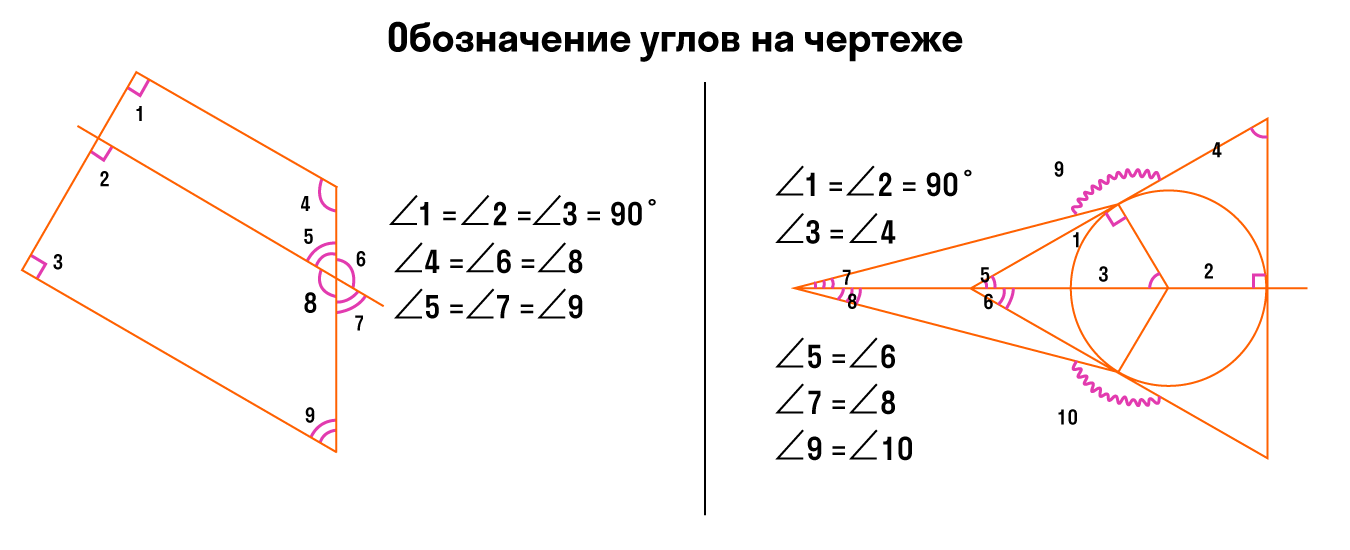
Как правильно измерять углы

Измерение углов похоже на измерение отрезков: нужно сравнить их с углом, принятым за единицу измерения. В геометрии обычно за единицу измерения принимают градус — угол, равный 1/180 части развернутого угла. Обозначается — 0.

Градусная мера угла — положительное число, которое показывает, сколько раз градус и его части укладываются в данном углу.

Есть еще две возможные меры угла: минуты и секунды. Они позволяют выполнять более точные расчеты, особенно, когда величина не является целым обозначением градуса.

Минута — 1/60 часть градуса. Обозначается — ´.

Секунда — 1/60 часть минуты. Обозначается — ´´.

Градус состоит из 3600 секунд, то есть: 1° = 60′ = 3600′.

Как происходит измерение угла: сначала измеряются стороны угла, а после его внутренняя область. Всегда нужно считать количество уложенных углов, так как они предопределяют меру измеряемого угла.

Когда луч делит угол на два или более углов, градусная мера всего угла равна сумме градусных мер этих углов.

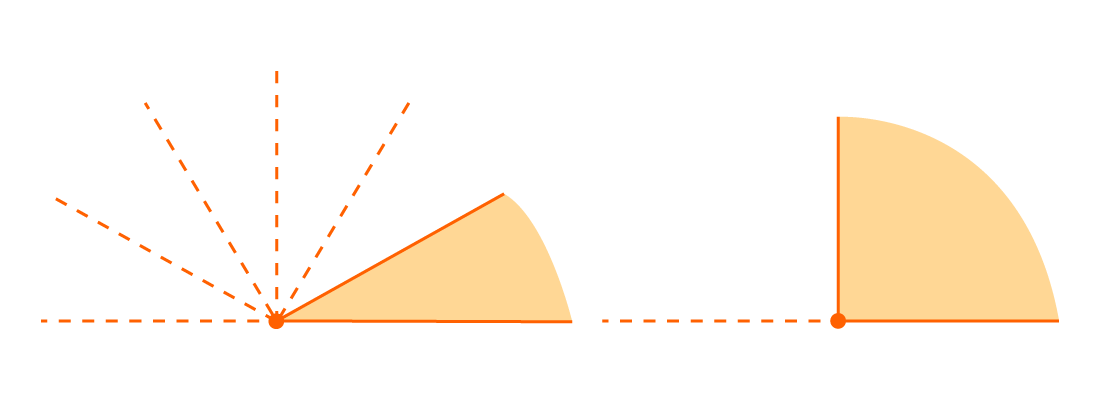
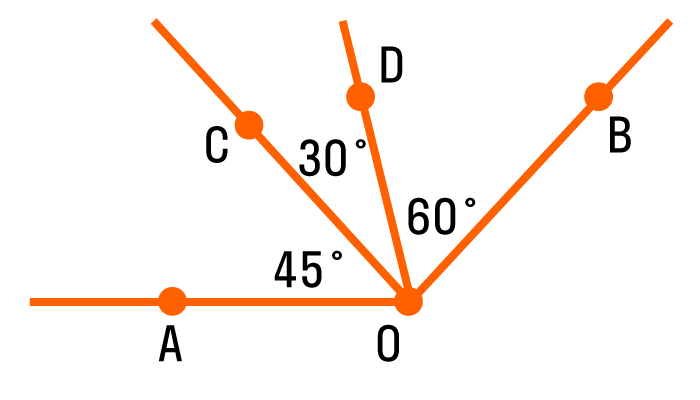
На рисунке изображен угол АОВ, он состоит из углов АОС, СОD и DОВ. Можно записать так: ∠ A O B = ∠ A O C + ∠ D O B = 45° + 30° + 60° = 135 °.

Угол называется прямым, если он равен 90°, а острым, если он меньше 90°, тупым, если он больше 90°, но меньше 180°. Развернутый угол имеет 180°.

Равные углы имеют равную градусную меру.

4. Угол наклона шкворня (поперечный) и дополнительный поперечный угол

Поперечный наклон шкворня отсчитывается от вертикали по направлению центральной оси автомобиля (А).

Многие системы подвески не имеют шкворня, в этом случае можно говорить о воображаемом наклоне шкворня, заменяемого осью, проходящей через центры шаровых опор.

Дополнительный угол складывается из угла развала и угла поперечного наклона шкворня (с учетом знаков). Оси угла развала и поперечного наклона шкворня пересекаются в некоторой точке. Если точка пересечения лежит ниже дорожного покрытия, то размер С представляет собой положительное плечо обкатки, если точка пересечения выше дорожного покрытия – плечо обкатки отрицательное.

Маленький радиус обкатки способствует стабилизации рулевого управления. На автомобилях с диагональным разделением контуров тормозов отрицательное плечо обкатки стабилизирует рулевое управление при неравном распределении тормозных сил на управляемых колесах.

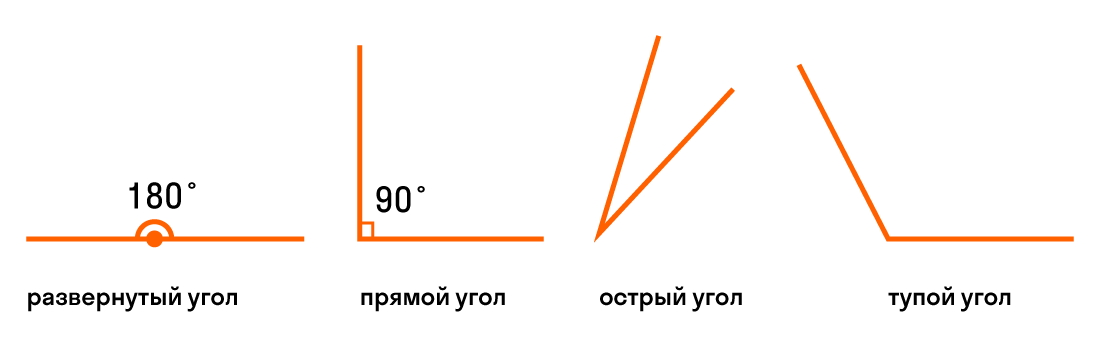
Направление поворота

Отметим на окружности с центром О точки А и А 1 . В точку А 1 возможно попасть, совершив точкой А поворот относительно центра О либо по часовой стрелке, либо – против. Очевидно определять эти повороты, как различные.

Принято считать, что поворот по часовой стрелке – поворот в отрицательном направлении направлении, а поворот против часовой стрелки – поворот в положительном направлении.

Приведем графическую иллюстрацию различных поворотов: слева на чертеже – поворот в положительном направлении; справа – в отрицательном.

Тригонометрические функции углового и числового аргумента

Каждому значению угла α соответствует определенное значение синуса и косинуса этого угла. Также, как всем углам α , отличным от α = 90 ° + 180 ° · k , k ∈ Z ( α = π 2 + π · k , k ∈ Z ) соответствует определенное значение тангенса. Котангенс, как сказано выше, определен для всех α , кроме α = 180 ° · k , k ∈ Z ( α = π · k , k ∈ Z ).

Можно сказать, что sin α , cos α , t g α , c t g α – это функции угла альфа, или функции углового аргумента.

Аналогично можно говорить о синусе, косинусе, тангенсе и котангенсе, как о функциях числового аргумента. Каждому действительному числу t соответствует определенное значение синуса или косинуса числа t. Всем числам, отличным от π 2 + π · k , k ∈ Z соответствует значение тангенса. Котангенс, аналогично, определен для всех чисел, кроме π · k , k ∈ Z.

Основные функции тригонометрии

Синус, косинус, тангенс и котангенс – основные тригонометрические функции.

Из контекста обычно понятно, с каким аргументом тригонометрической функции (угловой аргумент или числовой аргумент) мы имеем дело.

Циклическая частота вращения (обращения)

Скалярная величина, измеряющая частоту вращательного движения, называется циклической частотой вращения. Это угловая частота, равная не самому вектору угловой скорости, а его модулю. Ещё её именуют радиальной или круговой частотой.

Циклическая частота вращения – это количество оборотов тела за 2*π секунды.

У электрических двигателей переменного тока это частота асинхронная. У них частота вращения ротора отстаёт от частоты вращения магнитного поля статора. Величина, определяющая это отставание, носит название скольжения – S. В процессе скольжения вал вращается, потому что в роторе возникает электроток. Скольжение допустимо до определённой величины, превышение которой приводит к перегреву асинхронной машины, и её обмотки могут сгореть.

Устройство этого типа двигателей отличается от устройства машин постоянного тока, где токопроводящая рамка вращается в поле постоянных магнитов. Большое количество рамок вместил в себя якорь, множество электромагнитов составили основу статора. В трёхфазных машинах переменного тока всё наоборот.

При работе асинхронного двигателя статор имеет вращающееся магнитное поле. Оно всегда зависит от параметров:

• частоты питающей сети;
• количества пар полюсов.

Скорость вращения ротора состоит в прямом соотношении со скоростью магнитного поля статора. Поле создаётся тремя обмотками, которые расположены под углом 120 градусов относительно друг друга.

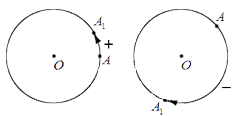
Обозначение углов на чертеже

Чертеж помогает решать задачки по геометрии в разы быстрее. Чтобы наглядно изображать дуги, углы и прочие фигурки, придумали даже отдельное направление — геометрический чертеж.

Задачи с углами могут быть разными и не всегда есть возможность правильно изобразить и отметить угол. Вот, что важно запомнить при обозначении лучей и углов:

• Равные углы обозначают одинаковым количеством дуг.
• Неравные углы обозначают разным количеством дуг, чтобы они отличались между собой.
• Для обозначения на чертеже более трех углов используем разные виды дуг: волнистые, зубчатые.

На чертеже отмечены острые, равные и неравные углы.

Обозначать углы можно разными цветами. Главное, чтобы было просто и броско. При этом необязательно отмечать все-все углы — достаточно только тех, которые нам нужны для решения задачки.

Бесплатный марафон: как самому создавать игры, а не только играть в них (◕ᴗ◕)

Записаться на марафон

• 0
• 0
• 0
• 0
• 0
• 0

Бесплатный марафон: как самому создавать игры, а не только играть в них (◕ᴗ◕)

5. Продольный наклон шкворня

Угол продольного наклона шкворня отсчитывается от вертикали при взгляде сбоку автомобиля.

Угол продольного наклона влияет на стабилизацию рулевого управления.

Для обеспечения тенденции к установке управляемых колес угол продольного наклона обычно делают положительным.

А вдруг автор этой статьи все придумал?

Если немного изменить матрицу, то можно получить вращение по спирали или сделать из точки маятник.

Связь определений sin, cos, tg и ctg из геометрии и тригонометрии

Вернемся к данным в самом начале определениям и углу альфа, лежащему в пределах от 0 до 90 градусов. Тригонометрические определения синуса, косинуса, тангенса и котангенса полностью согласуются с геометрическими определениями, данными с помощью соотношений сторон прямоугольного треугольника. Покажем это.

Возьмем единичную окружность с центром в прямоугольной декартовой системе координат. Повернем начальную точку A ( 1 , 0 ) на угол величиной до 90 градусов и проведем из полученной точки A 1 ( x , y ) перпендикуляр к оси абсцисс. В полученном прямоугольном треугольнике угол A 1 O H равен углу поворота α , длина катета O H равна абсциссе точки A 1 ( x , y ) . Длина катета, противолежащего углу, равна ординате точки A 1 ( x , y ) , а длина гипотенузы равна единице, так как она является радиусом единичной окружности.

В соответствии с определением из геометрии, синус угла α равен отношению противолежащего катета к гипотенузе.

sin α = A 1 H O A 1 = y 1 = y

Значит, определение синуса острого угла в прямоугольном треугольнике через соотношение сторон эквивалентно определению синуса угла поворота α , при альфа лежащем в пределах от 0 до 90 градусов.

Аналогично соответствие определений можно показать для косинуса, тангенса и котангенса.

Переход от угловой к линейной скорости

Существует различие между линейной скоростью точки и угловой скоростью. При сравнении величин в выражениях, описывающих правила вращения, можно увидеть общее между этими двумя понятиями. Любая точка В, принадлежащая окружности с радиусом R, совершает путь, равный 2*π*R. При этом она делает один оборот. Учитывая, что время, необходимое для этого, есть период Т, модульное значение линейной скорости точки В находится следующим действием:

ν = 2*π*R / Т = 2*π*R* ν.

Так как ω = 2*π*ν, то получается:

Следовательно, линейная скорость точки В тем больше, чем дальше от центра вращения находится точка.

К сведению. Если рассматривать в качестве такой точки города на широте Санкт-Петербурга, их линейная скорость относительно земной оси равна 233 м/с. Для объектов на экваторе – 465 м/с.

Числовое значение вектора ускорения точки В, движущейся равномерно, выражается через R и угловую скорость, таким образом:

а = ν2/ R, подставляя сюда ν = ω* R, получим: а = ν2/ R = ω2* R.

Это значит, чем больше радиус окружности, по которой движется точка В, тем больше значение её ускорения по модулю. Чем дальше расположена точка твердого тела от оси вращения, тем большее ускорение она имеет.

Поэтому можно вычислять ускорения, модули скоростей необходимых точек тел и их положений в любой момент времени.

Понимание и умение пользоваться расчётами и не путаться в определениях помогут на практике вычислениям линейной и угловой скоростей, а также свободно переходить при расчётах от одной величины к другой.

Видео

7. Задние управляемые колеса

В последнее время некоторые изготовители автомобилей вводят систему задних управляемых колес. В основном системы с задними управляемыми колесами сконструированы так, что при превышении скорости 30-50 км/ч задние колеса поворачиваются в ту сторону, что и передние (А). Более сложные системы обеспечивают поворот задних колес в противоположном направлении поворота передних на низких скоростях (В) и поворот в том же направлении на высоких.
Применение задних управляемых колес повышает управляемость автомобиля, способствует повышению скорости прохождения поворотов, улучшает маневренность при парковках.

До попыток отрегулировать рулевой привод задних управляемых колес, ознакомьтесь с руководством по обслуживанию вашего автомобиля.

8. Ось симметрии и отклонения осей

Осью симметрии называется линия, соединяющая центры передней и задней осей (А).

Неправильная установка схождения передних или задних колес может стать причиной отклонения движения автомобиля от заданного направления.

Нарушение симметрии называют отклонением осей.

9. Сдвижка колес

Сдвижка колес (Х) измеряется на колесах одной оси. Может измеряться в линейных и угловых мерах.

10. Установочная высота

Некоторые производители автомобилей требуют при проведении регулировочных работ обеспечения определенной загрузки автомобиля.

В зависимости от модели загрузка должна быть произведена на передних (А) и задних (В) сиденьях и багажнике (С).

11. Шины

Неправильная установка колес приводит к ускоренному износу шин. На рис. 11 показан характер износа шин при неправильной регулировке схождения: излишнее обратное схождение приводит к ступенчатому износу беговых дорожек (А) и износу внутренней части протектора (В)