Определение среднего углового ускорения

Вращение твердых тел и формулы углового ускорения

Все виды движения, с которыми человек сталкивается на протяжении своей жизни, изучаются в физике в рамках законов классической механики Ньютона. В данной статье речь пойдет о вращении твердых тел, об уравнениях, которые его описывают, и о формулах углового ускорения.

Как найти угол поворота формула

Законы, определяющие движение тела по окружности, аналогичны законам поступательного движения. Уравнения, описывающие вращательное движение, можно вывести из уравнений поступательного движения, произведя в последних следующие замены:

Если:
перемещение s — угловое перемещение (угол поворота) φ,
скорость u — угловая скорость ω,
ускорение a — угловое ускорение α

Угловая скорость и угловое ускорение

Рассмотрим понятия угловой скорости и углового ускорения при вращении твердого тела:

Угловое ускорение Как рассчитать и примеры

угловое ускорение это изменение, которое влияет на угловую скорость, принимая во внимание единицу времени. Он представлен греческой буквой альфа, α. Угловое ускорение является векторной величиной; следовательно, он состоит из модуля, направления и смысла.

Единицей измерения углового ускорения в Международной системе является радиан в секунду в квадрате. Таким образом, угловое ускорение позволяет определить, как угловая скорость изменяется во времени. Угловое ускорение, связанное с равномерно ускоренными круговыми движениями, часто изучается.

Таким образом, при равномерно ускоренном круговом движении значение углового ускорения является постоянным. Наоборот, при равномерном круговом движении значение углового ускорения равно нулю. Угловое ускорение эквивалентно в круговом движении тангенциальному или линейному ускорению при прямолинейном движении.

На самом деле его значение прямо пропорционально значению тангенциального ускорения. Таким образом, чем больше угловое ускорение колес велосипеда, тем больше испытываемое ускорение.

Следовательно, угловое ускорение присутствует как в колесах велосипеда, так и в колесах любого другого транспортного средства, при условии изменения скорости вращения колеса..

Аналогично, угловое ускорение также присутствует в колесе, поскольку оно испытывает равномерно ускоренное круговое движение, когда оно начинает свое движение. Конечно, угловое ускорение также можно найти в карусели.

• 1 Как рассчитать угловое ускорение?
  • 1.1 Равномерно ускоренное круговое движение
  • 1.2 Крутящий момент и угловое ускорение
  • 2.1 Первый пример
  • 2.2 Второй пример
  • 2.3 Третий пример

  В чем измеряется угловое ускорение? Пример задачи на вращение

  

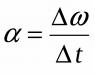
  Движение по окружности или вращательное перемещение твердых тел является одним из важных процессов, который изучают разделы физики – динамика и кинематика. Данную статью посвятим рассмотрению вопроса, в чем измеряется угловое ускорение, которое появляется во время вращения тел.

  Понятие об угловом ускорении. Формулы кинематики и динамики вращения. Пример задачи

  

  Вращение тел является одним из важных типов механического движения в технике и природе. В отличие от линейного перемещения, оно описывается собственным набором кинематических характеристик. Одной из них является угловое ускорение. Охарактеризуем эту величину в статье.

  Основные понятия

  Угловое ускорение – величина, характеризующая изменение скорости с течением времени.

  Пусть рассматриваемый промежуток времени это: Δ t = t 1 – t , а изменение угловой скорости составит Δ ω = ω 1 – ω , тогда числовое значение среднего углового ускорения за тот же интервал времени: " open=" ε = ∆ ω ∆ t = ε . Перейдем к пределу, когда Δ t > 0 , тогда формула углового ускорения будет иметь вид: ε = l i m ∆ t → 0 ∆ ω ∆ t = d ω d t = d 2 φ d t = ω ˙ = φ ¨ .

  Числовое значение ускорения в заданный момент времени есть первая производная от угловой скорости или вторая производная от угла поворота по времени.

  Размерность углового ускорения 1 T 2 (т.е. 1 в р е м я 2 ). Укажем также, в чем измеряется угловое ускорение: за единицу измерения стандартно принимается р а д / с 2 или иначе: 1 с 2 ( с – 2 ) .

  Ускоренное вращение тела – это вращение, при котором угловая скорость (ее модуль) возрастает с течением времени.

  Замедленное вращение тела – это вращение, при котором угловая скорость (ее модуль) убывает с течением времени.

  В общем, довольно просто заметить, что, если ω и ε имеют одинаковые знаки, наблюдается ускоренное вращение, а, когда противоположные знаки – замедленное.

  

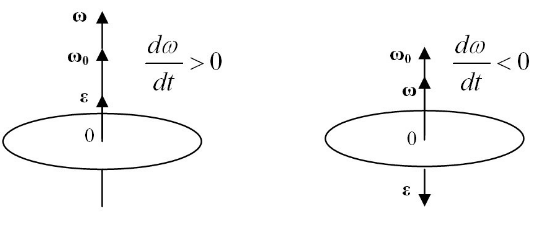
  Рисунок 1 . Вектор углового ускорения

  Если мы представим угловое ускорение как вектор ε → = d ω → d t , имеющий направление вдоль оси вращения, то в случае ускоренного вращения ε → и ω → совпадут по направлениям (левая часть
  рисунка 1 ) и будут противоположны по направлениям в случае замедленного вращения (правая часть
  рисунка 1 ).

  Понятие об угловом ускорении

  

  Очевидно, что прежде чем давать ответ на вопрос, в чем измеряется угловое ускорение в физике, следует познакомиться с самим понятием.

  В механике линейного движения ускорение играет роль меры быстроты изменения скорости и вводится в физику через второй закон Ньютона. В случае вращательного движения существует аналогичная линейному ускорению величина, которая называется ускорением угловым. Формула для его определения записывается в виде:

  То есть угловое ускорение α является первой производной угловой скорости ω по времени. Так, если скорость во время вращения не изменяется, то ускорение будет равно нулю. Если же скорость линейно зависит от времени, например, увеличивается постоянно, то ускорение α примет постоянное ненулевое положительное значение. Отрицательное значение α говорит о том, что система замедляет свое вращение.

  Как рассчитать угловое ускорение?

  В общем, мгновенное угловое ускорение определяется из следующего выражения:

  В этой формуле ω – угловая скорость вектора, а t – время.

  • Читайте также:

    Ящик в багажник авто

  Среднее угловое ускорение также можно рассчитать из следующего выражения:

  В частном случае плоского движения бывает, что как угловая скорость, так и угловое ускорение являются векторами с направлением, перпендикулярным плоскости движения..

  С другой стороны, модуль углового ускорения можно рассчитать по линейному ускорению с помощью следующего выражения:

  В этой формуле а – тангенциальное или линейное ускорение; и R – радиус вращения кругового движения.

  Круговое движение равномерно ускорено

  Как уже упоминалось выше, угловое ускорение присутствует в равномерно ускоренном круговом движении. По этой причине интересно знать уравнения, которые управляют этим движением:

  θ = θ₀ + ω₀ ∙ t + 0,5 ∙ α ∙ t 2

  В этих выражениях θ – угол, пройденный в круговом движении, θ₀ начальный угол, ω₀ начальная угловая скорость, а ω угловая скорость.

  

  Крутящий момент и угловое ускорение

  В случае линейного движения, согласно второму закону Ньютона, для того, чтобы тело приобрело определенное ускорение, требуется сила. Эта сила является результатом умножения массы тела и ускорения, которое испытало то же самое.

  • Читайте также:

    Японский двигатель на газель в актау

  Однако в случае кругового движения сила, необходимая для придания углового ускорения, называется крутящим моментом. Короче говоря, крутящий момент можно понимать как угловую силу. Обозначается греческой буквой τ (произносится «тау»).

  Аналогичным образом, необходимо учитывать, что во вращательном движении момент инерции I тела выполняет роль массы в линейном движении. Таким образом, крутящий момент кругового движения рассчитывается по следующему выражению:

  В этом выражении I – момент инерции тела относительно оси вращения.

  Вращение в природе и технике

  

  Прежде чем изучать угловое ускорение и формулы, которые позволяют его определить, рассмотрим, что представляет собой процесс вращения.

  Вам будет интересно: Сокровища – это. Значение слова, фильмы с этим словом и не только

  В физике под вращением понимают такой тип движения, при котором каждая точка тела произвольной формы или материальная точка движется по круговой траектории. Через центр этой траектории перпендикулярно ее плоскости проходит ось вращения. Рассматриваемый тип перемещения в пространстве может происходить с постоянной скоростью или с переменной. В последнем случае говорят о наличие у тела ускорения.

  Примерами вращения в быту являются движение лопастей вентилятора, вращение колес велосипеда и автомобиля, вращение ножей блендера или рабочей части миксера, движение валов и шестерен. В природе также можно наблюдать этот тип движения, например, перемещение нашей Земли вокруг Солнца и ее суточное вращение вокруг своей оси.

  Закон равнопеременного вращения

  Равнопеременное вращение – вращение, при котором угловое ускорение во все время движения является постоянным ( ε = c o n s t ) .

  • Читайте также:

    Японский аукцион автомобилей на русском без регистрации

  Выведем формульно закон равнопеременного вращения. Пусть в начальный момент времени t 0 угол вращения равен ϕ = ϕ 0 ; угловая скорость – ω = ω 0 (т.е. ω 0 является начальной угловой скоростью).

  Выражение ε = d ω d t = ω ˙ = φ ¨ дает нам возможность сделать запись: d ω = ε d t . Проинтегрируем левую часть крайней записи в пределах от ω 0 до ω , а правую – в пределах от 0 до t , тогда:

  ω = ω 0 + ε t , d φ = ω 0 d t + ε t d t .

  Проинтегрируем вторично и получим формулу, выражающую закон равнопеременного вращения:

  Закон равнопеременного вращения: φ = φ 0 + ω t + ε t 2 2 .

  Вращение является равноускоренным, когда ω и ε имеют одинаковые знаки.

  Вращение является равнозамедленным, когда ω и ε противоположны по знаку.

  Угловое ускорение имеет связь с полным и тангенциальным ускорениями. Пусть некоторая точка вращается неравномерно по окружности с радиусом R , тогда: α r = ε R . Нормальное ускорение имеет также связь с угловым: a n = ω 2 R . Учтем это выражение и для полного ускорения получим: a = a r 2 + a n 2 = R ε 2 + ω 4 Для равнопеременного движения: ω = ε t ; a n = ω 2 R = ε 2 t 2 R и a = R ε 2 + ε 4 t 4 = R ε 1 + ε 2 t 4 .

  Кинематические характеристики вращения

  К этим характеристикам относятся три величины: угловое ускорение, угловая скорость и угол поворота. Будем обозначать их греческими символами α, ω и θ соответственно.

  Так как тело движется по окружности, то удобно рассчитывать угол θ, на который оно повернется за определенное время. Этот угол выражается в радианах (реже в градусах). Поскольку окружность имеет 2 × pi радиан, то можно записать равенство, связывающее θ с длиной дуги L поворота:

  Где r – радиус вращения. Эту формулу несложно получить, если вспомнить соответствующее выражение для длины окружности.

  

  Угловая скорость ω, как и ее линейный аналог, описывает быстроту поворота вокруг оси, то есть она определяется согласно следующему выражению:

  Величина ω¯ является векторной. Направлена она вдоль оси вращения. Единицей ее измерения является радиан в секунду (рад/с).

  Наконец, угловое ускорение – это физическая характеристика, которая определяет быстроту изменения величины ω¯, что математически записывается так:

  Вектор α¯ направлен в сторону изменения вектора скорости ω¯. Далее будет сказано, что угловое ускорение направлено в сторону вектора момента силы. Измеряют эту величину в радианах в квадратную секунду (рад/с 2 ).

  Угол поворота

  Во всех уравнения вращательного движения углы задаются в радианах, сокращенно (рад).

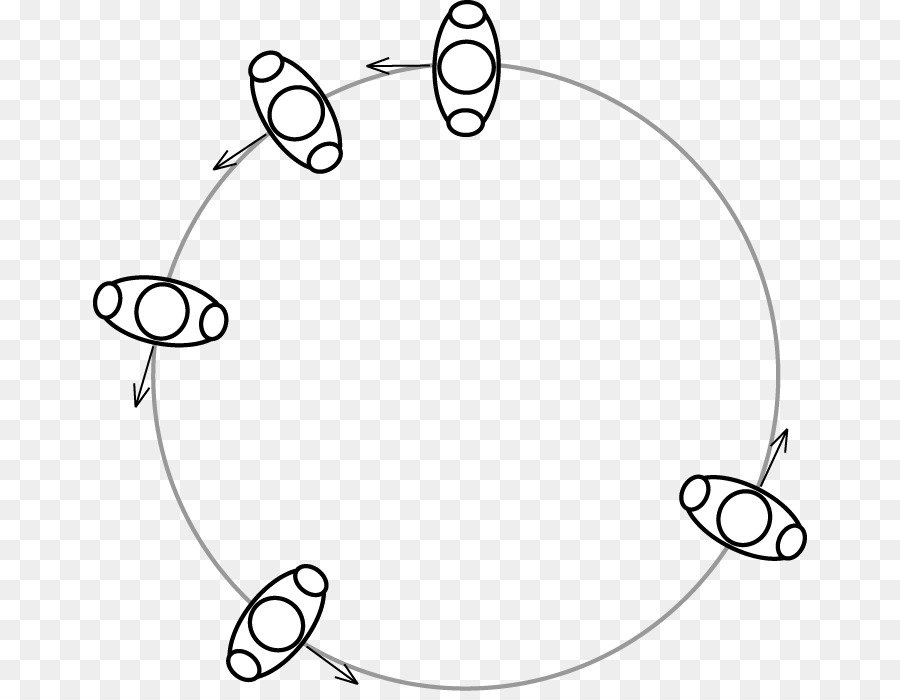
  Если
  φ — угловое перемещение в радианах,
  s — длина дуги, заключенной
  между сторонами угла поворота,
  r — радиус,
  то по определению радиана

  Соотношение между единицами угла

  Обратите внимание: Наименование единицы радиан (рад) обычно указывается в формулах только в тех случаях, когда ее можно спутать с градусом. Поскольку радиан равен отношению длин двух отрезков
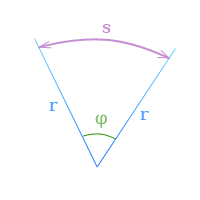
  ( 1 рад = 1 м/ 1 м = 1 ), он не имеет размерности.

  Соотношение между угловой скоростью, угловым перемещением и временем для всех видов движения по окружности наглядно видны на графике угловой скорости (зависимость ω от t). 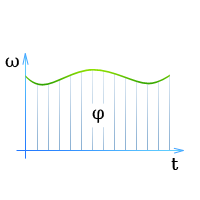Поэтому графику можно определить, какой угловой скоростью обладает тело в тот или иной момент времени и на какой угол с момента начала движения оно повернулось (он характеризуется площадью под кривой).

  Кроме того, для представления соотношений между названными величинами используют график углового перемещения (зависимость φ от t) и график углового ускорения (зависимость α от t).

  Динамика вращения

  

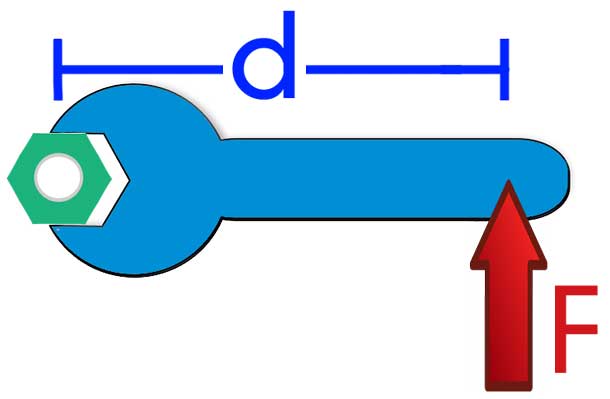
  В физике всякое ускорение возникает только тогда, когда существует ненулевая внешняя сила, действующая на тело. В случае движения вращения эта сила заменяется на момент силы M, равный произведению плеча d на модуль силы F. Известное уравнение моментов динамики вращательного перемещения тел записывается в следующем виде:

  Здесь I – момент инерции, играющий ту же роль в системе, что и масса во время линейного перемещения. Эта формула позволяет вычислить величину α, а также определить, в чем измеряется угловое ускорение. Имеем:

  Мы получили единицу измерения α из уравнения моментов, тем не менее, ньютон не является базовой единицей СИ, поэтому его следует заменить. Для выполнения этой задачи воспользуемся вторым законом Ньютона, получаем:

  Мы получили ответ на вопрос, в каких единицах измеряется угловое ускорение. Оно измеряется в обратных квадратных секундах. Секунда, в отличие от ньютона, является одной из семи основных единиц СИ, поэтому полученная единица для α используется при математических расчетах.

  Полученная единица измерения для углового ускорения является правильной, однако, по ней трудно понять физический смысл величины. В связи с этим поставленную задачу можно решить иным способом, используя при этом физическое определение ускорения, которое было записано в предыдущем пункте.

  примеров

  Первый пример

  Определить мгновенное угловое ускорение движущегося тела, совершающего вращательное движение, с учетом выражения его положения во вращении Θ (t) = 4 т. 3 я. (Где i – единичный вектор в направлении оси x).

  Также определите значение мгновенного углового ускорения, когда прошло 10 секунд с начала движения..

  решение

  Выражение угловой скорости можно получить из выражения положения:

  ω (t) = d Θ / dt = 12 т 2 я (рад / с)

  Как только мгновенная угловая скорость была вычислена, мгновенное угловое ускорение может быть вычислено как функция времени.

  α (t) = dω / dt = 24 t i (рад / с) 2 )

  Чтобы вычислить значение мгновенного углового ускорения по истечении 10 секунд, необходимо только заменить значение времени в предыдущем результате..

  α (10) = = 240 i (рад / с) 2 )

  Второй пример

  Определите среднее угловое ускорение тела, которое испытывает круговое движение, зная, что его начальная угловая скорость была 40 рад / с и что через 20 секунд она достигла угловой скорости 120 рад / с..

  решение

  Из следующего выражения вы можете рассчитать среднее угловое ускорение:

  Третий пример

  Каково будет угловое ускорение колеса, которое начинает двигаться с равномерно ускоренным круговым движением, пока через 10 секунд оно не достигнет угловой скорости в 3 оборота в минуту? Каким будет тангенциальное ускорение кругового движения в этот период времени? Радиус колеса составляет 20 метров.

  решение

  Во-первых, необходимо преобразовать угловую скорость из оборотов в минуту в радианы в секунду. Для этого выполняется следующее преобразование:

  ω_F = 3 об / мин = 3 ∙ (2 ∙ Π) / 60 = Π / 10 рад / с

  Как только это преобразование выполнено, можно рассчитать угловое ускорение, учитывая, что:

  Π / 10 = 0 + α ∙ 10

  α = Π / 100 рад / с 2

  А тангенциальное ускорение возникает в результате действия следующего выражения:

  Какими величинами описывают вращение?

  Вам будет интересно: Троллейбус – это городской вид транспорта

  Поскольку рассматриваемый вид движения происходит по круговой траектории, то оказывается удобным описать его с помощью величин, которые используют величину угла кругового сектора. Перечислим эти величины.

  Угол θ – это центральный угол кругового сектора. Для наглядности он показан ниже на рисунке.

  

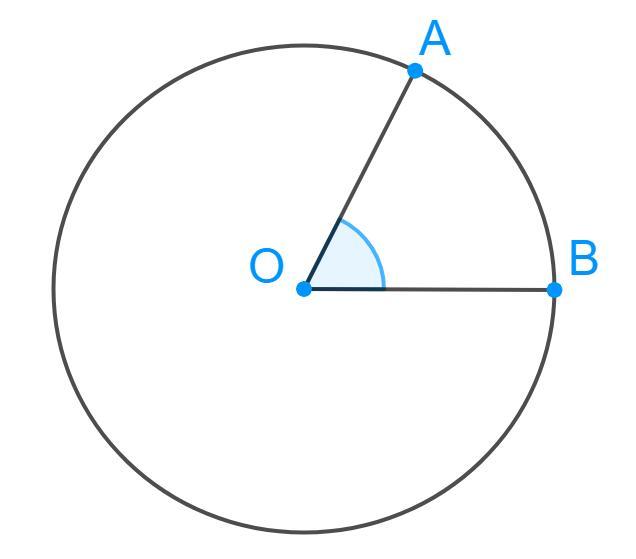
  Здесь дуга AB – это расстояние, которое прошло вращающееся тело за некоторый промежуток времени t. Используя соответствующую пропорцию, можно получить связь между длиной этой дуги L и углом θ, выраженным в радианах. Эта связь имеет следующий математический вид:

  Символом r обозначен радиус окружности. Напомним, что один оборот по круговой траектории соответствует углу θ = 2 × pi.

  Следующая важная кинематическая величина вращения – это скорость. Ее, как правило, обозначают греческой буквой ω (омега) и определяют в радианах в секунду. Отличие этой скорости, которая называется угловой, от ее линейного аналога является очевидным, поскольку последняя измеряется в метрах в секунду. Математически величина ω определяется так:

  То есть угловая скорость показывает быстроту поворота тела. Записанное выражение называется мгновенной скоростью, вычисленной в бесконечно малый промежуток времени (t; t + dt). Формула для средней скорости ωm запишется в виде:

  При этом на угловом промежутке θ мгновенная скорость ω может значительно изменяться.

  Наконец, третьей важной величиной, которая используется для описания неравномерного движения по окружности, является угловое ускорение α. Эта величина показывает как изменяется скорость на данном промежутке времени. Формула углового ускорения через скорость угловую выглядит следующим образом:

  Отсюда следует, что единицей измерения α является радиан в квадратную секунду (рад/с2).

  Число оборотов

  Характеристикой всех видов вращения является число оборотов n или равноценная ей характеристика — частота f. Обе величины характеризуют число оборотов в единицу времени.

  Единица СИ частоты (или числа оборотов)

  В технике число оборотов обычно измеряется в оборотах в минуту (об/мин) = 1/мин.

  Таким образом, величина, обратная числу оборотов, есть продолжительность одного оборота.

  Если
  n — число оборотов,
  f — частота,
  T — продолжительность одного оборота, период,
  φ — угловое перемещение,
  N — полное число оборотов,
  t — время, продолжительность вращения,
  ω — угловая частота,
  то

  Период

  Угловое перемещение

  Угловое перемещение равно произведению полного числа оборотов на 2π:

  Угловая скорость

  Из формулы для одного оборота следует:

  Обратите внимание:
  • формулы (1)—(6) справедливы для всех видов вращательного движения — как для равномерного движения, так и для ускоренного. В них могут входить постоянные величины, средние значения, начальные и конечные значения, а также любые мгновенные значения.
  • вопреки своему названию число оборотов n — это не число, а физическая величина.
  • следует различать число оборотов n и полное число оборотов N.

  Движение по окружности — простейший случай криволинейного движения тела. Когда тело движется вокруг некоторой точки, наряду с вектором перемещения удобно ввести угловое перемещение ∆ φ (угол поворота относительно центра окружности), измеряемое в радианах.

  Зная угловое перемещение, можно вычислить длину дуги окружности (путь), которую прошло тело.

  Если угол поворота мал, то ∆ l ≈ ∆ s .

  

  Угловые скорость и ускорение

  Вернемся к определению углового ускорения. В кинематике вращения угловая скорость определяет угол поворота за единицу времени. В качестве единиц измерения угла можно использовать либо градусы, либо радианы. Последние чаще применяются. Таким образом, угловая скорость измеряется в радианах в секунду или сокращенно рад/с.

  Поскольку угловое ускорение – это производная по времени от величины ω, то для получения его единиц измерения достаточно разделить на секунду единицу для ω. Последнее означает, что величина α будет измеряться в радианах за квадратную секунду (рад/с 2 ). Так, 1 рад/с 2 означает, что за каждую секунду вращения угловая скорость будет возрастать на 1 рад/с.

  Рассматриваемая единица для α аналогична той, которая была получена в предыдущем пункте статьи, где значение радиан было опущено, поскольку оно подразумевается в соответствии с физическим смыслом углового ускорения.

  Угловое и центростремительное ускорения

  

  Ответив на вопрос, в чем измеряется угловое ускорение (формулы приведены в статье), полезно также понять, как оно связано с центростремительным ускорением, которое является неотъемлемой характеристикой любого вращения. Ответ на этот вопрос звучит просто: угловое и центростремительное ускорения – это совершенно разные величины, которые являются независимыми.

  Ускорение центростремительное обеспечивает лишь искривление траектории тела во время вращения, угловое же ускорение приводит к изменению линейной и угловой скоростей. Так, в случае равномерного движения по окружности угловое ускорение равно нулю, центростремительное же ускорение имеет некоторую постоянную положительную величину.

  Угловое ускорение α связано с линейным касательным ускорением a следующей формулой:

  Где r – радиус окружности. Подставляя в это выражение единицы измерения для a и r, мы также получим ответ на вопрос, в чем измеряется угловое ускорение.

  Кинематические уравнения

  

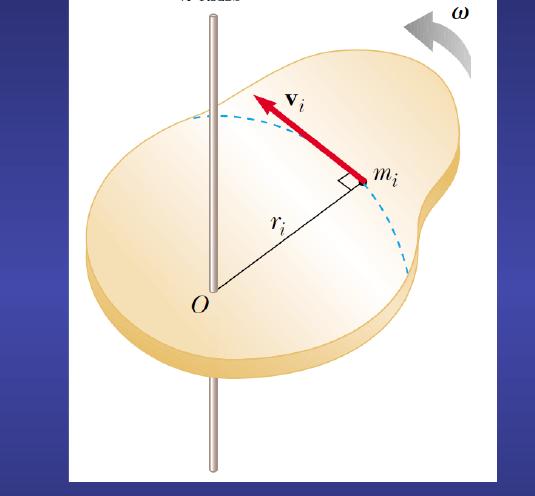
  Чтобы понять, какую важную роль играет угловое ускорение для описания движения вращения, запишем формулы, связывающие изученные выше кинематические величины.

  В случае равноускоренного вращения справедливы следующие математические соотношения:

  Первая формула показывает, что угловая скорость будет расти во времени по линейному закону. Второе выражение позволяет рассчитать угол, на который повернется тело за известное время t. Графиком функции θ(t) является парабола. В обоих случаях угловое ускорение – это постоянная величина.

  Если воспользоваться приведенной в начале статьи формулой связи между L и θ, то можно получить выражение для α через линейное ускорение a:

  Если α является постоянным, то при возрастании расстояния от оси вращения r будет пропорциональным образом увеличиваться линейное ускорение a. Именно поэтому для вращения пользуются угловыми характеристиками, в отличие от линейных, они не изменяются с увеличением или уменьшением r.

  Решение задачи

  Решим следующую задачу из физики. На материальную точку действует касательная к окружности сила 15 Н. Зная, что эта точка имеет массу 3 кг и вращается вокруг оси с радиусом 2 метра, необходимо определить ее угловое ускорение.

  

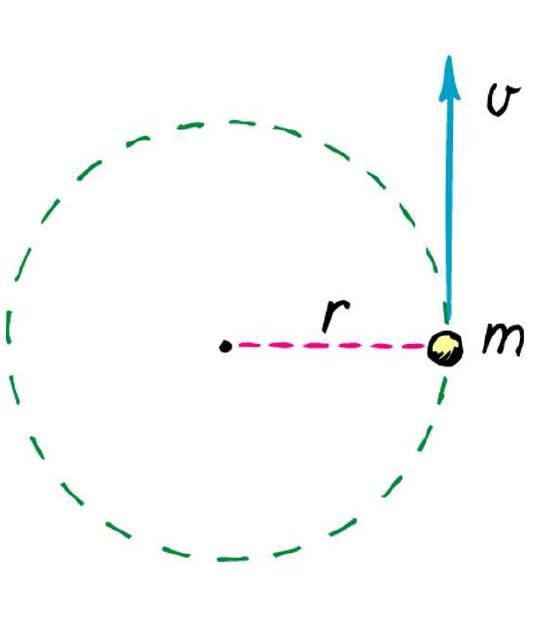
  Решается эта задача с использованием уравнения моментов. Момент силы в данном случае равен:

  Момент инерции точки рассчитывается по следующей формуле:

  Тогда значение ускорения будет равно:

  Таким образом, за каждую секунду движения материальной точки скорость ее вращения будет увеличиваться на 2,5 радиана в секунду.

  Связь между линейным и угловым ускорением

  

  Линейное ускорение a показывает прирост скорости v за время t. Эта величина измеряется в метрах в секунду квадратную, то есть:

  Чтобы найти связь между величинами a и α обратимся к следующей формуле, приведенной ранее:

  Возьмем производную от левой и правой части равенства по времени, получим:

  Возьмем еще раз производную по dt:

  Мы получили формулу связи линейного и углового ускорений. Выражение показывает, что при постоянном ускорении α, величина a будет возрастать линейно с увеличением радиуса вращения.

  Равномерно ускоренное движение по окружности без начальной угловой скорости

  Тело начинает двигаться из состояния покоя, и его угловая скорость равномерно возрастает.

  

  ? — мгновенная угловая скорость тела в момент времени t
  ? — угловое ускорение, постоянное в течение времени t
  ? — угловое перемещение тела за время t, (? в радианах)
  t — время

  Поскольку на графике скорости угловое перемещение равно площади треугольника, имеем:

  Поскольку вращение тела начинается из состояния покоя, изменение угловой скорости ?? равно достигнутой в результате ускорения угловой скорости ?. Поэтому формула принимает следующий вид:

  

  Неравномерно ускоренное движение тела по окружности

  Движение тела по окружности будет неравномерно ускоренным, если изменение угловой скорости происходит не пропорционально времени, т. е. если угловое ускорение не остается постоянным. В этом случае и угловая скорость и угловое ускорение являются функциями времени.

  Связь величин ?, ? и ? представлена на соответствующих графиках.

  

  Мгновенная угловая скорость

  Полный угол поворота тела в любой момент времени можно определить по графику углового перемещения. Чем круче график, тем больше в данный момент времени мгновенная угловая скорость.

  ? — угол между касательной и осью времени t
  ? — мгновенная угловая скорость
  ? — угловое перемещение к моменту времени t

  

  Мгновенной угловой скоростью называется первая производная функции ? = ?(t) по времени.

  Обратите внимание:
  1) чтобы вычислить мгновенную угловую скорость ?, необходимо знать зависимость углового перемещения от времени.
  2) формула углового перемещения при равномерном движении тела по окружности и формула углового перемещения при равномерно ускоренном движении по окружности без начальной угловой скорости являются частными случаями формулы (2) соответственно для ? = 0 и ? = const.

  Из формул следует:

  Проинтегрировав обе части выражения, получим

  Угловое перемещение есть интеграл по времени от угловой скорости.

  

  Обратите внимание:
  Для вычисления углового перемещения ? необходимо знать зависимость угловой скорости от времени.

  Векторные величины, характеризующие вращательное движение тела

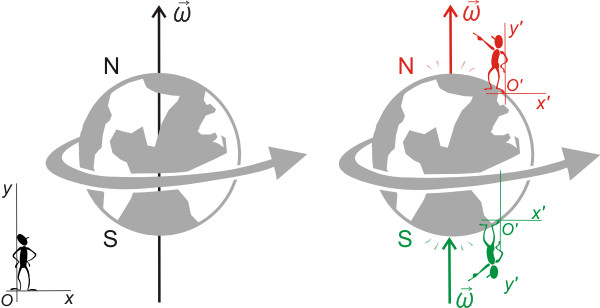
  Угловая скорость и угловое ускорение тела являются векторными величинами. Эти векторы направлены вдоль оси вращения (аксиальные векторы), а их длина определяет величину соответствующих характеристик вращательного движения. Направление векторов определяется по правилу буравчика, т. е. совпадает с направлением поступательного движения буравчика, рукоятка которого движется в том же направлении, что и тело.

  Определение:Если тело участвует одновременно в нескольких вращательных движениях, то результирующая угловая скорость определяется по правилу векторного (геометрического) сложения:

  Величина результирующей угловой скорости определяется по аналогии с формулой (Сложение движений):

  или, если оси вращения перпендикулярны друг другу

  Примечание: Результирующее угловое ускорение определяется аналогичным образом. Графически результирующую можно найти как диагональ параллелограмма скоростей или ускорений.